http://acm.pku.edu.cn/JudgeOnline/problem?id=1178
Задача: Камелот
Давным давно король Артур и рыцари Круглого Стола обычно собирались на новый год, чтобы отпраздновать свою дружбу. В память об этих событиях придумали настольную игру "Камелот" для одного игрока, в которой Король и несколько фигур Рыцарей произвольно располагаются в различных клетках доски.
Доска имеет размер 8х8 клеток, как показано ниже на рисунке.
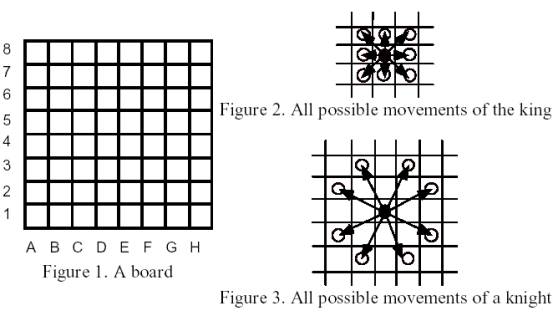
Король может перемещаться в любую смежную клетку доски из закрашенной окружности в не закрашенную, как показано на рисунке Figure 2, при этом не выходя за пределы доски.
Рыцарь может перемещаться из клетки с закрашенной окружностью в одну из клеток с незакрашенной окружностью, как показано на рисунке Figure 3, при этом не выходя за пределы доски.
Во время игры может поместить более одной фигуры в одну клетку. Клетки считаются достаточно большими, и не возникает препятствий для свободного перемещения фигур.
Игроку необходимо так перемещать фигуры Короля и Рыцарей, чтобы собрать их всех в какой-то одной клетке за наименьшее число ходов. Ходы фигурами необходимо делать по правилам, описанным выше. Дополнительно к этому, если Король и оди или более Рыцарей находятся в одной клетке, игрок может Короля и одного из рыцарей переместить вместе по правилам перемещения Рыцаря и считать это одним ходом.
Напишите программу для вычисления минимального количества ходов, необходимых для перемещения всех фигур в одну клетку доски.
Входные данные
Все входные данне размещены в одной строке, описывающей начальное расоложение фигур на доске. Строка сожержит последовательность клеток доски, первая из которых - клетка Короля, остальные - клетки Рыцарей. Каждая клетка описывается парой "буква-цифра". Буква обозначает горизонтальную, а цифра - вертикальную координату клетки доски. Все фигуры в начале игры расположены в разных клетках.
0 <= количество Рыцарей <= 63
Выходные данные
Вывести единственную строку с положительным целым числом, обозначающим минимальное число ходов игрока, необходимых для перемещения всех фигур в одну клетку доски.
Пример входных данных
D4A3A8H1H8
Пример выходных данных
10
Идея решения
Методом "волны" (обходом в ширину) подсчитаем минимальное количество ходов, за которое Рыцарь может попасть из клетки с координатами (x, y) в клетку (i, j). Сделаем это для всех пар клеток и запомним результаты в четырехмерной матрице p[1..8, 1..8, 1..8, 1..8]. Количество ходов для Короля из клетки (x, y) в клетку (i, j) равно Max(Abs(i-x), Abs(j-y)). Если запретить совместное перемещение Короля и Рыцаря, то задача с водится к поиску клетки (i, j), сумма расстояний до которого от клеток, занимаемых Королем и Рыцарями, имеет минимальное значение. Предположим, что в клетке (xp, yp) Король встречается с Рыцарем, имеющим номер k, и дальнейшее перемещение до клетки (i, j) они выполняют совместно. В этом случае требуется подсчитать количество ходов Короля от клетки (xk, yk) до (xp, yp) и прибавить к нему величины p[x[k], y[k], xp, yp] и p[xp, yp, i, j]. Проделав эту работу для всех пар (i, j) и (xp, yp), не забывая при этом фиксировать минимальную оценку, мы получим искомый результат.
Зная алгоритмическую классику - задачи о расстановке ферзей, обхода конем шахматной доски, поиска выхода из лабиринта и т.п. - решение данной задачи найти не сложно. Ее можно рассматривать как обобщение на идейном уровне и использовать для самостоятельной работы при изучении темы "Перебор и методы его сокращения". Интерпретация же доски в виде графа позволяет установить связь с такими известными алгоритмами поиска кратчайших путей, как алгоритмы Дейкстра и Флойда, именно последний использован нами в примере решения на С++.
Решение на Pascal:
const TW = 8;
TW2 = 2*TW;
NKMAX = 63;
UNKNOWN = -1;
type Board = array[0..TW-1,0..TW-1] of integer;
BigBoard = array[0..TW2-1,0..TW2-1] of integer;
BigString= string[255];
var NK : integer; (* # knights *)
IP : array[0..2*NKMAX-1] of integer; (* input *)
MCM: array[0..NKMAX-1] of Board; (* cost matrices for matings *)
KingMat : Board;
KMats : array[0..TW-1,0..TW-1] of Board; (* all-pos knights costs *)
KBoard: BigBoard;
function CL(c:char):integer; (* chess letter *)
begin
CL := ord(c) - ord('A');
end;
function CD(c:char):integer; (* chess digit *)
begin
CD := ord(c) - ord('1');
end;
procedure Erase(var t:Board);
var h,v:integer;
begin
for h:=0 to TW-1 do
for v:=0 to TW-1 do
t[h,v] := UNKNOWN;
end;
procedure AddBoard(a,b: Board; var c:Board);
var v,h:integer;
begin
for v:=0 to TW-1 do
for h:=0 to TW-1 do
c[h,v] := a[h,v]+b[h,v];
end;
procedure KnightCosts(h,v,s:integer; var t:Board);
begin
if(h>=0) and (h<TW) and (v>=0) and (v<TW) then
if (t[h,v]<0) or (s<t[h,v]) then
begin
t[h,v] := s;
inc(s);
KnightCosts(h+2,v+1,s,t);
KnightCosts(h+2,v-1,s,t);
KnightCosts(h-2,v+1,s,t);
KnightCosts(h-2,v-1,s,t);
KnightCosts(h+1,v+2,s,t);
KnightCosts(h+1,v-2,s,t);
KnightCosts(h-1,v+2,s,t);
KnightCosts(h-1,v-2,s,t);
end;
end;
procedure KingCosts(h,v,s:integer; var t:Board);
var j:integer;
begin
if(h>=0) and (h<TW) and (v>=0) and (v<TW) then
if (t[h,v]<0) or (s<t[h,v]) then
begin
t[h,v] := s;
inc(s);
KingCosts(h,v+1,s,t);
KingCosts(h,v-1,s,t);
for j:=-1 to 1 do
begin
KingCosts(h+1,v+j,s,t);
KingCosts(h-1,v+j,s,t);
end
end
end;
(* PreCompute Knight cost matrices for all 64 board positions *)
procedure ComputeKnightMats;
var h,v:integer;
begin
for v := 0 to TW-1 do
for h := 0 to TW-1 do
begin
Erase(KMats[h,v]);
KnightCosts(h,v,0,KMats[h,v]);
end;
end;
(* The cost matrix for Knight at h,v *)
procedure GetKnightCostMat(h,v:integer; var k:Board);
begin
k := KMats[h,v];
end;
(* Minimum value of Board and Position *)
function MinVal(k:Board):integer;
var v,h,S:integer;
begin
S:=k[0,0];
for v:=0 to TW-1 do
for h:=0 to TW-1 do
if(k[h,v]<S) then
S:=k[h,v];
MinVal := S;
end;
(* Compute the matings cost matrices for all NK knights *)
(* *)
(* MCM[i] = combined cost of king mating Knight i *)
procedure MakePairs;
var i,ii,h,v: integer;
tb,km,tu,kmt:Board;
begin
for i:=0 to NK-1 do
begin
ii := i*2;
GetKnightCostMat(IP[ii],IP[ii+1],km);
AddBoard(km,KingMat,tb);
for h:=0 to TW-1 do
for v:=0 to TW-1 do
begin
GetKnightCostMat(h,v,kmt);
AddBoard(tb,kmt,tu);
MCM[i][h,v]:=MinVal(tu);
end;
end
end;
procedure Results(val:integer);
var i:integer;
begin
writeln(val);
end;
(* Pick the Best *)
function Best:integer;
var allknights,rn,someknight: Board;
i,newval,val,ii,h,v: integer;
begin
(* first case, no gathering *)
GetKnightCostMat(IP[0],IP[1],allknights);
ii := 2;
for i:=1 to NK-1 do
begin
GetKnightCostMat(IP[ii],IP[ii+1],someknight);
AddBoard(allknights,someknight,allknights);
inc(ii,2);
end;
(* rs = sum of all knight matrices *)
AddBoard(allknights,KingMat,rn);
val := MinVal(rn); (* first guess, no matings *)
(* now, the NK possible matings *)
ii := 0;
for i:=0 to NK-1 do (* mate with knight i *)
begin
GetKnightCostMat(IP[ii],IP[ii+1],someknight);
(* someknight = costs of Knight i *)
for h:=0 to TW-1 do (* rn = rs - kt + MCM[i] *)
for v:=0 to TW-1 do
rn[h,v] := allknights[h,v] - someknight[h,v] + MCM[i][h,v];
newval := MinVal(rn);
if(newval<val)then
val := newval;
inc(ii,2);
end;
{writeln(val);}
Best :=val;
end;
procedure ReadPieces;
var buf: bigstring;
i : integer;
begin
readln(buf);
KingCosts(CL(buf[1]),CD(buf[2]),0,KingMat);
i := 3; NK := 0;
while(i<length(buf))do
begin
IP[i-3]:=CL(buf[i]);
inc(i);
IP[i-3]:=CD(buf[i]);
inc(i);
inc(NK);
end;
end;
procedure InitData;
begin
Erase(KingMat);
ComputeKnightMats;
end;
begin
InitData;
ReadPieces;
MakePairs;
Results(Best)
end.Решение на С++:
#include <iostream>
using namespace std;
const int inf = 100000;
char str[150];
int k[64],king[64][64],knight[64][64];
int move1[8][2]={-1,-1,-1,0,-1,1,0,1,1,1,1,0,1,-1,0,-1};
int move2[8][2]={-1,-2,-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2};
void init(){
int i,j,x,y,tx,ty;
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(i==j) king[i][j]=knight[i][j]=0;
else king[i][j]=knight[i][j]=inf;
for(i=0;i<64;i++){
x=i/8,y=i%8;
for(j=0;j<8;j++){
tx=x+move1[j][0],ty=y+move1[j][1];
if(tx>=0 && ty>=0 && tx<8 && ty<8)
king[i][8*tx+ty]=1;
}
}
for(i=0;i<64;i++){
x=i/8,y=i%8;
for(j=0;j<8;j++){
tx=x+move2[j][0],ty=y+move2[j][1];
if(tx>=0 && ty>=0 && tx<8 && ty<8)
knight[i][8*tx+ty]=1;
}
}
}
void floyd1(){
int i,j,k;
for(k=0;k<64;k++)
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(king[i][k]+king[k][j]<king[i][j])
king[i][j]=king[i][k]+king[k][j];
}
void floyd2(){
int i,j,k;
for(k=0;k<64;k++)
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(knight[i][k]+knight[k][j]<knight[i][j])
knight[i][j]=knight[i][k]+knight[k][j];
}
int main(){
int i,j,l,cnt,pos,sum,ans,len,t1,t2;
init();
floyd1();
floyd2();
while(scanf("%s",str)!=EOF){
len=strlen(str);
pos=(str[0]-'A')+(str[1]-'1')*8;
cnt=(len-2)/2;
if(cnt==0){
printf("0\n");
continue;
}
for(i=0,j=2;i<cnt;i++,j+=2)
k[i]=(str[j]-'A')+(str[j+1]-'1')*8;
for(ans=inf,i=0;i<64;i++){
for(sum=l=0;l<cnt;l++)
sum+=knight[k[l]][i];
for(j=0;j<64;j++){
t1=king[pos][j];
for(t2=inf,l=0;l<cnt;l++)
t2=min(t2,knight[k[l]][j]+knight[j][i]-knight[k[l]][i]);
ans=min(ans,sum+t1+t2);
}
}
printf("%d\n",ans);
}
return 0;
}