http://acm.pku.edu.cn/JudgeOnline/problem?id=1179
Задача: Полигон
Существует игра для одного игрока, которая начинается с задания Полигона с N вершинами. Ниже на рисунке приведен пример графического предоставления Полигона при N = 4. Для каждой вершины Полигона задается значение - целое число, а для каждого ребра - метка операции "+" (сложение), либо "*" (умножение).
Ребра Полигона пронумерованы от 1 до N.
Первых ходом в игре удаляется одно из ребер.
Каждый последующий ход состоит из следующих шагов:
- выбирается ребро Е и две вершины V1 и V2, которые соединены ребром Е;
- ребро Е и вершины V1 и V2 заменяються новой вершиной со значением, равным результату выполнения операции, определенной меткой ребра Е, над значениями вершины V1 и V2.
Игра заканчивается, когда больше нет ни одного ребра. Результат игры - это число, равное значению оставшейся вершины.
Пример игры. Рассмотрим полигон, приведенный в условии задачи.
Игрок начал игру с удаления ребра 3 (рисунок ниже). После этого игрок выбирает ребро 1, затем - ребро 4 и, наконец, ребро 2. Результатом будет число 0.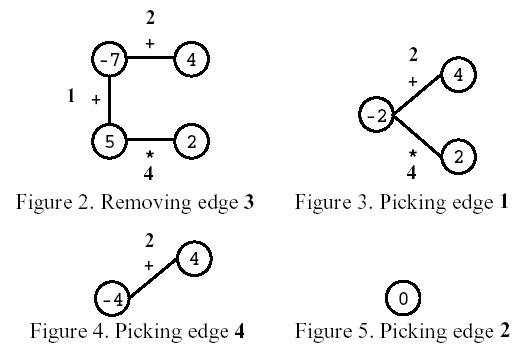
Требуется написать программу, которая по заданному Полигону вычисляет максимальное значение оставшейся вершины и выводит список всех ребер, удаление которых на первом ходе игры позволяет получить это значение.
Входные данные
Входные данные опис ывают полигон с N вершинами. Данные содержаться в 2-х строках. В первой строке записано число N. Вторая строка содержит метки ребер с номерами 1, ..., N, между которыми записаны через один пробел значения вершин (первое из них соответствует вершине, смежной ребрам 1 и 2, следующее - смежной 2 и 3, и так далее, последнее - смежной ребрам N и 1). Метка ребра - это буква t, соответствующая операции "+" или буква x, соответствующая операции "*".
3 <= N <= N50
Для любой последовательности ходов значения вершин находятся в пределах [ -32768, 32767 ]
Выходные данные
В первой строке выходных данных выведите максимальное значение оставшейся вершины, которое может быть достигнуто для заданного Полигона. Во второй строке должен быть записан список всех ребер, удаление которых на первом ходе позволяет получить это значение. Номера ребер должны записываться в возрастающем порядке и отделяться друг от друга пробелом.
Пример входных данных\
4
t -7 t 4 x 2 x 5
Пример выходных данных
33
1 2
Обсуждение задачи
Рассмотрим более простой вариант задачи. Пусть операции в вершинах неотрицательны, а на ребрах мы сами выбираем операцию "+" или "*". Из значений в вершинах (операндов) и операций составляется арифметическое выражение. Задача сводиться к такой расстановке скобок в арифметическом выражении, чтобы результат вычисления этого выражения был максимальным.
Пусть у нас есть строка s, описывающая конкретное выражение. Подзадача - это решение задачи для строки с i-го по j-й операнд. Получив один раз результат для подзадачи, мы затем в неизменном виде (без пересчета) используем его для решения подзадач большей размерности (выражения большей длины). В массиве W мы при этом храним результаты решения подзадач; W[i, j] равно максимальному значению выражения, полученному при решении задачи для подстроки s[i..j]. Значение W[i, i] рвно i-му операнду. Очевидно, что W[i, j] = 0 при i > j. Особенность заполнения массива W заключается в том, что он заполняется по диагоналям, параллельным главным: j - i = 0, j - i = 1, j - i = 2, ..., j - i = N-1. Принцип такого заполнения описывается следующими рекуррентными соотношениями:
W[i, j] = s[i] при i = j, 1 <= i, j <= N.
W[i, j] = Max(W[i, k] * W[k+1, j], W[i, k] + W[k+1, j]) при i < j
Вернемся к исходной задаче. После удаления первого ребра остается выражение, в котором необходимо расставить скобки так, чтобы его значение было максимальным. В отличие от предыдущей задачи, здесь знаки операций уже заданы. Например, пусть в примере из формулировки задачи удалено первое ребро. Остается выражение: -7 + 4 * 2 * 5. Элемент массива W[i, j], исходя из особенностей задачи, мы теперь определим несколько иначе, а именно - как максимальное значение длины j, начинающегося с операнда i. Так, W[1, 3] равно максимальному значению выражения -7 + 4 * 2, достигаемого при проверке всех способов расстановки скобок. Очевидно, что W[i, 1] равно значению операнда i.
Теперь явно просматривается традиционная динамическая схема. Единственная сложность - отрицательные числа: при их умножении может быть получен максимум. В силу этого необходимо ввести аналогичный массив V для хранения минимальных значений и также рассчитывать их для каждого выражения.
Ответом в задаче является максимальное (максимальные) значение (значения) в последнем столбце W. При этом номера строк указывают те ребра исходного графа, удаление которых позволяет получить эти значения.
Решение на Pascal:
const
minVert = 3;
maxVert = 50;
antMaxVert = maxVert - 1;
opSum = 't';
type
polygonT = record
vert: array[0..antMaxVert] of char;
side: array[0..antMaxVert] of integer;
numVert: minVert..maxVert
end;
maxminT = record
maxVal, minVal: integer
end;
memoryT = array[1..maxVert, 0..antMaxVert] of maxminT;
scoresT = record
scor: array[1..maxVert] of integer;
numVert, highScor, firstVertHS: integer;
end;
var
polygon: polygonT;
scores: scoresT;
procedure ReadPolygon (var P: polygonT);
var
i: integer;
c: char;
begin
with P do
begin
readln(numVert);
for i := 0 to numVert - 2 do
read(vert[i], side[i], c);
read(vert[numVert - 1], side[numVert - 1]);
end
end;
procedure Evaluate (Op: char; E1, E2: maxminT; var MM: maxminT);
var
values: array[1..4] of integer;
i, indMax, indMin: integer;
begin
if Op = opSum then
begin
MM.maxVal := E1.maxVal + E2.maxVal;
MM.minVal := E1.minVal + E2.minVal
end
else
begin
values[1] := E1.maxVal * E2.maxVal;
values[2] := E1.maxVal * E2.minVal;
values[3] := E1.minVal * E2.maxVal;
values[4] := E1.minVal * E2.minVal;
indMax := 1;
indMin := 1;
for i := 2 to 4 do
if values[i] > values[indMax] then
indMax := i
else if values[i] < values[indMin] then
indMin := i;
MM.maxVal := values[indMax];
MM.minVal := values[indMin]
end
end;
procedure CompScores (var P: polygonT; var M: memoryT);
var
lastVert, line, inf, infRight, dimLeft: integer;
mmTemp, mmAux: maxminT;
begin
lastVert := P.numVert - 1;
(* Line 1 --- expressions with one integer *)
for inf := 0 to lastVert do
begin
M[1, inf].maxVal := P.side[inf];
M[1, inf].minVal := P.side[inf]
end;
(* Line 2 --- expressions with two integers *)
for inf := 0 to lastVert do
begin
infRight := (inf + 1) mod P.numVert;
if P.vert[infRight] = opSum then
M[2, inf].maxVal := M[1, inf].maxVal + M[1, infRight].maxVal
else
M[2, inf].maxVal := M[1, inf].maxVal * M[1, infRight].maxVal;
M[2, inf].minVal := M[2, inf].maxVal
end;
(* Line 3 ... Line P.numVert *)
for line := 3 to P.numVert do
for inf := 0 to lastVert do
begin
infRight := (inf + 1) mod P.numVert;
Evaluate(P.vert[infRight], M[1, inf], M[line - 1, infRight], mmTemp);
for dimLeft := 2 to line - 1 do
begin
infRight := (inf + dimLeft) mod P.numVert;
Evaluate(P.vert[infRight], M[dimLeft, inf], M[line - dimLeft,
infRight], mmAux);
if mmAux.maxVal > mmTemp.maxVal then
mmTemp.maxVal := mmAux.maxVal;
if mmAux.minVal < mmTemp.minVal then
mmTemp.minVal := mmAux.minVal
end;
M[line, inf] := mmTemp
end
end;
procedure CompHighScores (var P: polygonT; var S: scoresT);
var
mem: memoryT;
i, maxScor, fstVert: integer;
begin
CompScores(P, mem);
S.scor[1] := mem[P.numVert, 0].maxVal;
maxScor := S.scor[1];
fstVert := 1;
for i := 2 to P.numVert do
begin
S.scor[i] := mem[P.numVert, i - 1].maxVal;
if S.scor[i] > maxScor then
begin
maxScor := S.scor[i];
fstVert := i
end
end;
S.numVert := P.numVert;
S.highScor := maxScor;
S.firstVertHS := fstVert
end;
procedure WriteResults (var S: scoresT);
var
i: integer;
begin
with S do
begin
writeln(highScor : 1);
write(firstVertHS : 1);
for i := firstVertHS + 1 to numVert do
if scor[i] = highScor then
write(' ', i : 1);
writeln
end
end;
begin
ReadPolygon(polygon);
CompHighScores(polygon, scores);
WriteResults(scores);
end.Решение на С++:
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 55;
int ans[MAXN];
int n, a[MAXN], b[MAXN];
char str1[MAXN], str2[MAXN];
int min(int a,int b){if(a<=b) return a;else return b;}
int max(int a,int b){if(a>=b) return a;else return b;}
void input()
{
char s[10];
scanf("%d", &n);
for(int i = 0; i < n; i ++) {
scanf("%s %d",s, &a[i]);
str1[i] = s[0];
}
}
int DP()
{
int i, j, k,r;
int dp[MAXN][MAXN][2];
for(i = 0; i < n; i ++)
dp[i][i][0] = dp[i][i][1] = b[i];
for(r=2;r<=n;r++)
{
for(i=0;i<=n-r;i++)
{
j=i+r-1;
dp[i][j][0]=INT_MAX;
dp[i][j][1]=INT_MIN;
for(k=i;k<j;k++)
{
if(str2[k]=='t')
{
dp[i][j][0]=min(dp[i][j][0],dp[i][k][0]+dp[k+1][j][0]);
dp[i][j][1]=max(dp[i][j][1],dp[i][k][1]+dp[k+1][j][1]);
}
else
{
int t=dp[i][j][0];
t=min(t,dp[i][k][0]*dp[k+1][j][0]);
t=min(t,dp[i][k][0]*dp[k+1][j][1]);
t=min(t,dp[i][k][1]*dp[k+1][j][1]);
t=min(t,dp[i][k][1]*dp[k+1][j][0]);
dp[i][j][0]=t;
t=dp[i][j][1];
t=max(t,dp[i][k][0]*dp[k+1][j][0]);
t=max(t,dp[i][k][0]*dp[k+1][j][1]);
t=max(t,dp[i][k][1]*dp[k+1][j][1]);
t=max(t,dp[i][k][1]*dp[k+1][j][0]);
dp[i][j][1]=t;
}
}
}
}
return dp[0][n - 1][1];
}
int main()
{
input();
int i, j, mx = INT_MIN;
for(i = 0; i < n; i ++)
{
for(j = 0; j < n; j ++)
{
b[j] = a[(i + j) % n];
if(j < n-1) str2[j] = str1[(i + j + 1) % n];
}
ans[i] = DP();
if(mx < ans[i]) mx = ans[i];
}
printf("%d\n", mx);
for(i = 0; i < n; i ++)
if(mx == ans[i]) printf("%d ", i + 1 );
printf("\n");
return(0);
}